蒙特卡洛树搜索
Published:
蒙特卡洛树搜索
基本概念
蒙特卡洛树搜索算法是一种基于模拟的搜索算法,通常用于人工智能领域的游戏和规划问题中。
蒙特卡洛树搜索基于两个核心思想:模拟和树搜索。在模拟和搜索中,算法通过将大量的随机模拟运用到搜索树来优化树的生长。其大致过程为:从根节点开始,每次迭代时选择一个未被完全扩展的节点,然后通过随机模拟产生一个搜索树的新节点,这个过程一直持续到达终端状态。
蒙特卡洛树搜索包含四个过程:
- 选择(Selection)
- 扩展 (expansion)
- 模拟(Simulation)
- 回溯(Backpropagation)
选择
在蒙特卡洛树搜索中,我们将每个节点分为三类:
- 未访问:还没有评估过当前局面
- 未完全展开:被评估过至少一次,但是子节点(下一步的局面)没有被全部访问过,可以进一步扩展
- 完全展开:子节点被全部访问过
我们根据一定的策略选择一个子树。选择的依据可以根据UCB算法,蒙特卡洛树会选择UCB值最高的子树并进入该子树。
\[UCB = \frac{w_i}{n_i} + c\sqrt[]{\frac{logN_i}{n_i}}\]其中,$w_i$是 i 节点的胜利次数,$n_i$ 是i节点的模拟次数,$N_i$是所有模拟次数,c 是探索常数,理论值为√2,可根据经验调整,c 越大就越偏向于广度搜索,c 越小就越偏向于深度搜索,加号的前面部分就是胜率,然后加号的后面部分函数长这样:
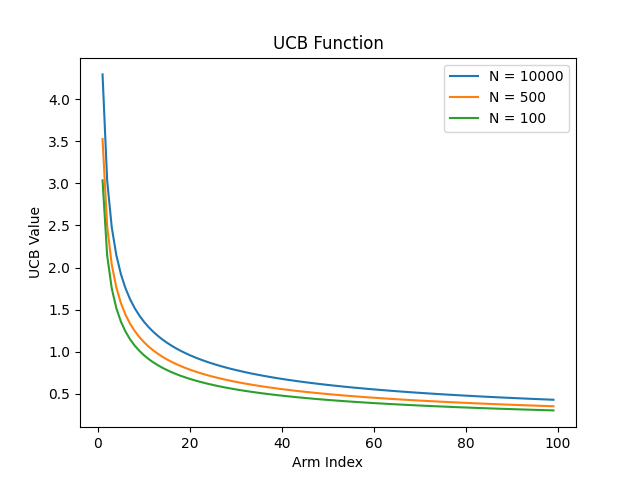
随着访问次数的增加,加号后面的值越来越小,因此我们的选择会更加倾向于选择那些还没怎么被统计过的节点,避免了蒙特卡洛树搜索会碰到的陷阱——一开始走了歪路。
UCB值通过衡量历史的平均回报和当前状态的不确定性(标准偏差)之间的折衷来实现此目标。具体计算方法为:将对历史奖励的平均值与当前选项的不确定性进行加权混合,以确定该选项的最佳选择。其目的是尽可能利用历史的奖励记录,同时探索不确定性较高的选项,以便找到最佳选择。
扩展
根据我们上一步的选择,找到了一个节点。在这个搜索到的存在未扩展的子节点,加上一个0/0的子节点,表示没有历史记录参考。这时我们进入第三步。
模拟
模拟会进行快速走子,每次模拟只走一盘,分出个胜负。 我们每个节点(每个节点代表每个不同的局面)都有两个值,代表这个节点以及它的子节点模拟的次数和赢的次数,比如模拟了 10 次,赢了 4 盘,记为 4/10。
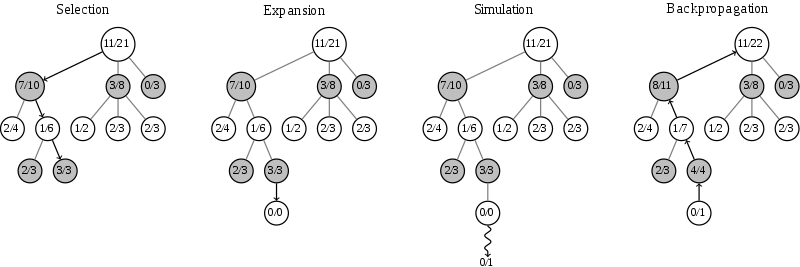
回溯
第四步是回溯(backpropagation), 将我们最后得到的胜负结果回溯加到MCTS树结构上。注意除了之前的MCTS树要回溯外,新加入的节点也要加上一次胜负历史记录,如上图最右边所示。
